 I was listening to WYUR the other night, when the host starting calling people on his phone list (he actually called me, but my phone was on 'vibrate' and not in my pocket). But he dialed the numbers on air. Now, WYUR has this superstrict policy about not discussing any indentifiable personal info on the air, such as full names, AIM screen names, and telephone numbers. I always figured that I could listen to the dialed numbers, and, by pushing telephone buttons, work out what numbers were dialed. However, this is harder than it sounds (ha!).
I was listening to WYUR the other night, when the host starting calling people on his phone list (he actually called me, but my phone was on 'vibrate' and not in my pocket). But he dialed the numbers on air. Now, WYUR has this superstrict policy about not discussing any indentifiable personal info on the air, such as full names, AIM screen names, and telephone numbers. I always figured that I could listen to the dialed numbers, and, by pushing telephone buttons, work out what numbers were dialed. However, this is harder than it sounds (ha!).Telephone tones use something called DTMF which stands for "Dual-Tone Multi-Frequency." In short, it means that sound for each number on the telephone keypad is made up of two frequencies. For example, 1 is a combination of a 697Hz signal with a 1209Hz signal. If you go here [wikipedia], you'll see that when looking across a row the numbers share the low frequency and vary the high frequency, whereas when you look down a column, the numbers share the high frequency and vary the low.
Why is all this important? Well, it means that although it is often easier to tell the difference between a 1 and a 2 by listening, it is not as easy to hear the difference between a 1 and a 4. This is because humans hearing (generally) is most sensitive to frequencies in the 1000-4000Hz range, meaning that with notes sharing a higher frequency the changes in the lower frequencies are much harder to perceive. So, since I couldn't do it by ear: Enter FFT - "Fast Fourier Transform."
[People who may be scared by somewhat mathy/physicsy stuff may want to skip till after the pictures]
At the risk of scaring more people off, I will briefly explain what Fourier Transforms (FTs) "do." I'll use sound for this example, since that is what the end goal in this case is. Basically, when you look at a sound - which is caused by something vibrating - you usually look at the movement of the vibrating stuff as it varies through time. Alternatively, you could also look at what 'amount' of which frequencies of vibration are present in that sound. A FT is a mathematical mechanism of switching between those two views.
If you have a recorded audio signal, which is a measurement of the vibration, and you apply a FT to that signal, you will get a measure of the frequencies in the audio, instead. (As a side note, in Quantum Mechanics, FTs are often used to switch between a momentum distribution and a position distribution.) A FFT is simply "an efficient algorithm to compute" the FT - in other words, it's faster than doing a FT directly.
At the risk of scaring more people off, I will briefly explain what Fourier Transforms (FTs) "do." I'll use sound for this example, since that is what the end goal in this case is. Basically, when you look at a sound - which is caused by something vibrating - you usually look at the movement of the vibrating stuff as it varies through time. Alternatively, you could also look at what 'amount' of which frequencies of vibration are present in that sound. A FT is a mathematical mechanism of switching between those two views.
If you have a recorded audio signal, which is a measurement of the vibration, and you apply a FT to that signal, you will get a measure of the frequencies in the audio, instead. (As a side note, in Quantum Mechanics, FTs are often used to switch between a momentum distribution and a position distribution.) A FFT is simply "an efficient algorithm to compute" the FT - in other words, it's faster than doing a FT directly.
For example, this is what a dialed 4 looks like in vibration-land:
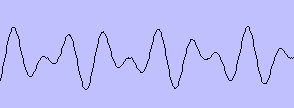
And this is what it looks like in frequency land. Notice the peaks at 770Hz and 1209 (I used Log frequency scale to see the peaks clearer, even if the exact frequency peak is hard to see by eye, but the computer picks out the peaks exactly):

So, (Finally! Whew!) using Audacity's FFT tool, I picked out which frequencies were in each of the dialed notes, matched them up with the frequency chart, and got the entire dialed number: 1-414-....
Take that WYUR!
Take that WYUR!
[PS. Audacity is a really great FREE! program]

You left out the most important way to have "Fun with FFT and DTMF" and that is playing "Happy Birthday to You" on your phone.
ReplyDeleteSo, are you saying we should all use rotary phones because then you can't tell what numbers are being dialed on air?
ReplyDeleteMaybe dial tone phones are another government conspiracy to figure out who is calling who.
I don't know, Uncle Sysfrog - it seems that it would be much easier to count clicks than use a FFT.
ReplyDeleteAnd in the spirit of "Word of the Day:" qdhewaoq.
true, if one could hear the clicking over the radio. However, dial tones are much louder (than clicking)over the radio and thus, easier to figure out what the phone number is.
ReplyDeleteYou are dangerous.
ReplyDelete